深度优先遍历(Depth First Search)的主要思想是首先以一个未被访问过的顶点作为起始顶点,沿当前顶点的边走到未访问过的顶点。当没有未访问过的顶点时,则回到上一个顶点,继续试探别的顶点,直至所有的顶点都被访问过。
下图示例的图从 0 开始遍历顺序如右图所示:
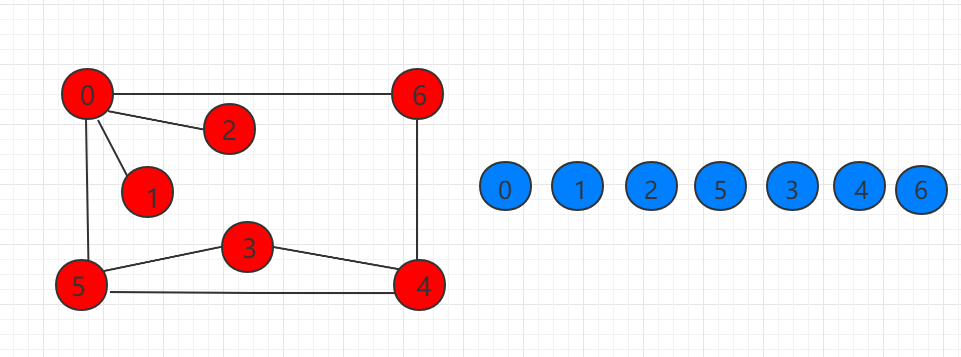
无向图 G 的一个极大连通子图称为 G 的一个连通分量(或连通分支)。连通图只有一个连通分量,即其自身;非连通的无向图有多个连通分量。连通分量与连通分量之间没有任何边相连。深度优先遍历可以用来求连通分量。
下面以求连通分量为例,来实现图的深度优先遍历,称为 dfs。下面代码片段中,visited 数组记录 dfs 的过程中节点是否被访问,ccount 记录联通分量个数,id 数组代表每个节点所对应的联通分量标记,两个节点拥有相同的 id 值代表属于同一联通分量。
...
// 构造函数, 求出无权图的联通分量
public Components(Graph graph){
// 算法初始化
G = graph;
visited = new boolean[G.V()];
id = new int[G.V()];
ccount = 0;
for( int i = 0 ; i < G.V() ; i ++ ){
visited[i] = false;
id[i] = -1;
}
// 求图的联通分量
for( int i = 0 ; i < G.V() ; i ++ )
if( !visited[i] ){
dfs(i);
ccount ++;
}
}
...图的深度优先遍历是个递归过程,实现代码:
...
// 图的深度优先遍历
void dfs( int v ){
visited[v] = true;
id[v] = ccount;
for( int i: G.adj(v) ){
if( !visited[i] )
dfs(i);
}
}
...Java 实例代码
src/runoops/graph/Components.java 文件代码:
实例
package runoops.graph;
import runoops.graph.read.Graph;
/**
* 深度优先遍历
*/
public class Components {
Graph G; // 图的引用
private boolean[] visited; // 记录dfs的过程中节点是否被访问
private int ccount; // 记录联通分量个数
private int[] id; // 每个节点所对应的联通分量标记
// 图的深度优先遍历
void dfs( int v ){
visited[v] = true;
id[v] = ccount;
for( int i: G.adj(v) ){
if( !visited[i] )
dfs(i);
}
}
// 构造函数, 求出无权图的联通分量
public Components(Graph graph){
// 算法初始化
G = graph;
visited = new boolean[G.V()];
id = new int[G.V()];
ccount = 0;
for( int i = 0 ; i < G.V() ; i ++ ){
visited[i] = false;
id[i] = -1;
}
// 求图的联通分量
for( int i = 0 ; i < G.V() ; i ++ )
if( !visited[i] ){
dfs(i);
ccount ++;
}
}
// 返回图的联通分量个数
int count(){
return ccount;
}
// 查询点v和点w是否联通
boolean isConnected( int v , int w ){
assert v >= 0 && v < G.V();
assert w >= 0 && w < G.V();
return id[v] == id[w];
}
} 自学教程
自学教程
分享笔记